Precision is a measure of consistency or agreement between scores and concerns the degree to which errors of measurement affect test scores.

Measurement errors do not usually refer to inconsistencies in the aptitudes or behaviors being assessed; rather, these errors are related to factors that prevent an individual from achieving a score identical to their true latent ability or score.

There are many ways in which precision can be measured. In traditional test theory, precision is measured by a reliability coefficient, which is the ratio of true score variance to observed score variance (Lord & Novick, 1968) (See Figure 1).

Figure 1

ASVAB - Test Score Precision - Figure 1

Because true score variance can be computed as the difference between observed score variance and error variance, classical reliability can be represented as seen in Figure 2.

Figure 2

ASVAB - Test Score Precision - Figure 2

Item Response Theory (IRT)

Item Response Theory (IRT) provides a means of estimating reliability that operates on the item characteristics and the individual pattern of responses given by examinees to items within a test. The IRT analogue to classical reliability is called marginal reliability, and operates on the variance of the theta scores and the average of the expected error variance (Sireci, Thissen, & Wainer, 1991) (Figure 3).

Figure 3

If it can be safely assumed that theta is distributed N(0,1), then marginal reliability can be measured as seen in Figure 4.

When sample sizes are large, the average of the expected error variance can be computed by averaging the variance of the estimated posterior distributions across individuals. In the reliabilities reported below, the posterior standard deviation (PSD) for individual i was estimated using the methodology given in Bock and Mislevy (1982) (Figure 5).

Figure 4

ASVAB - Test Score Precision - Figure 4

Figure 5

Figure 6

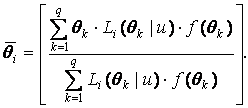
ASVAB Reliabilties

For each ASVAB subtest, the equation shown in Figure 6 was used to compute EAP ability estimates for applicants that completed the test during the 2009 fiscal year (FY2009; October 1, 2008 — September 30, 2009). The equation shown in Figure 5 was then used to compute PSDs (using the EAP ability estimates, and assuming a N(0,1) population distribution). The average of the squared PSDs was then computed over applicants, and substituted into the equation shown in Figure 4 to compute subtest reliability.

For AFQT scores, reliability was computed using the methodology for computing composite reliabilities reported in Gulliksen (1987; pg. 346-347, Equation 74).

Reliability estimates were computed over all FY2009 applicants, and by gender (Male, Female), ethnic group (Hispanic, Non-Hispanic), and race (American-Indian/Alaska Native, Asian, Black/African-American, Native Hawaiian/other Pacific Islander, White/Caucasian).

The sample sizes used to compute the reliability estimates across subtests and AFQT scores are given in the table below.

Sample Sizes Used to Compute ASVAB Reliability & SEM Estimates
Group P&P CAT
All 164,354 320,988
Male
Female		 124,201
40,138		 259,249
61,730
White Hispanic
Non-Hispanic		   12,649
108,496		    51,173
221,274
American-Indian
Asian
Black
Pacific Islander
White		 2,8502,42331,2901,55682,084     6,772
8,94340,5903,570208,814

The estimated reliabilities for AFQT scores and the subtests that comprise AFQT scores are reported in the table below.

Learn more about: AFQT Scores | ASVAB Subtests

Estimated Reliabilities for AFQT Scores & the AFQT Subtests
AFQT AR WK PC MK
Group P&P CAT P&P CAT P&P CAT P&P CAT P&P CAT
All 0.94 0.97 0.87 0.92 0.88 0.93 0.75 0.85 0.85 0.93
Male
Female		 0.94
0.94		 0.97
0.97		 0.87
0.86		 0.92
0.92		 0.88
0.88		 0.93
0.93		 0.75
0.75		 0.85
0.86		 0.85
0.85		 0.93
0.93
Hispanic
Non-Hispanic		 0.94
0.94		 0.97
0.97		 0.87
0.87		 0.92
0.92		 0.88
0.88		 0.92
0.93		 0.76
0.75		 0.86
0.85		 0.85
0.85		 0.92
0.93
American-Indian
Asian
Black
Pacific Islander
White		 0.94
0.93
0.94
0.94
0.94		 0.97
0.96
0.97
0.97
0.97		 0.87
0.87
0.85
0.85
0.88		 0.92
0.91
0.91
0.92
0.92		 0.88
0.87
0.89
0.88
0.88		 0.93
0.91
0.92
0.92
0.93		 0.75
0.75
0.76
0.76
0.74		 0.85
0.86
0.86
0.86
0.85		 0.85
0.85
0.84
0.84
0.85		 0.93
0.93
0.92
0.93
0.93

The estimated reliabilities for the remaining ASVAB subtests are given in the table below. Note that AI and SI are administered as separate subtests in CAT-ASVAB, but combined into one single score (labeled AS). AI and SI are combined into one single subtest (AS) in P&P-ASVAB. Scores on the combined subtest (AS) are reported for both CAT-ASVAB and P&P-ASVAB.

Estimated Reliabilities for the Non-AFQT Subtests
GS EI AI SI AS MC AO
Group P&P CAT P&P CAT P&P CAT P&P CAT P&P CAT P&P CAT P&P CAT
All 0.80 0.87 0.74 0.87 n/a 0.87 n/a 0.84 0.81 n/a 0.79 0.85 0.84 0.82
Male
Female		 0.81
0.79		 0.79
0.87		 0.74
0.72		 0.87
0.85		 n/a
n/a		 0.88
0.83		 n/a
n/a		 0.84
0.82		 0.83
0.74		 n/a
n/a		 0.80
0.76		 0.85
0.84		 0.83
0.85		 0.82
0.84
Hispanic
Non-Hispanic		 0.79
0.80		 0.86
0.88		 0.73
0.74		 0.86
0.87		 n/a
n/a		 0.85
0.87		 n/a
n/a		 0.82
0.84		 0.78
0.81		 n/a
n/a		 0.78
0.79		 0.84
0.85		 0.84
0.84		 0.83
0.82
American-Indian
Asian
Black
Pacific Islander
White		 0.81
0.77
0.78
0.79
0.81		 0.88
0.86
0.86
0.87
0.88		 0.74
0.71
0.71
0.72
0.75		 0.87
0.86
0.85
0.86
0.87		 n/a
n/a
n/a
n/a
n/a		 0.87
0.85
0.84
0.86
0.87		 n/a
n/a
n/a
n/a
n/a		 0.85
0.82
0.82
0.83
0.84		 0.82
0.76
0.74
0.79
0.84		 n/a
n/a
n/a
n/a
n/a		 0.79
0.76
0.76
0.77
0.80		 0.85
0.84
0.83
0.84
0.85		 0.83
0.83
0.86
0.84
0.83		 0.81
0.81
0.85
0.82
0.82

ASVAB Standard Errors of Measurement

The standard error of measurement (SEM) provides an alternate way of summarizing the amount of error or inconsistency in test scores. Figure 7 shows how this is computed, where  is the observed score standard deviation for test x. If the measurement error is normally distributed and the reported scores are unbiased, then the true scores for approximately 68% of the applicants would fall in the interval created by adding and subtracting one SEM from their reported score.

Figure 7

The SEM of each ASVAB subtest and AFQT score was computed over all FY2009 applicants, and by gender (Male, Female), ethnic group (Hispanic, Non-Hispanic), and race (American-Indian/Alaska Native, Asian, Black/African-American, Native Hawaiian/other Pacific Islander, White/Caucasian). The sample sizes are shown above.

The SEMs for AFQT scores and the subtests that comprise AFQT scores are reported in the table below.

Standard Errors of Measurement for AFQT Scores & AFQT Subtests
AFQT AR WK PC MK
Group P&P CAT P&P CAT P&P CAT P&P CAT P&P CAT
All 5.89 4.28 2.98 2.35 2.91 2.26 3.80 2.84 2.96 2.02
Male
Female		 5.93
5.69		 4.28
4.21		 3.00
2.79		 2.33
2.29		 2.90
2.92		 2.25
2.23		 3.88
3.56		 2.88
2.65		 3.03
2.76		 2.04
1.91
Hispanic
Non-Hispanic		 5.72
5.91		 4.43
4.17		 2.80
3.01		 2.34
2.31		 2.99
2.90		 2.49
2.13		 3.69
3.82		 2.96
2.76		 2.87
2.99		 2.15
1.96
American-Indian
Asian
Black
Pacific Islander
White		 5.76
6.58
5.39
6.01
5.81		 3.99
4.87
4.17
4.31
4.18		 2.86
3.14
2.87
3.17
2.85		 2.16
2.63
2.33
2.34
2.28		 2.79
3.78
2.70
3.27
2.80		 2.01
2.95
2.18
2.32
2.18		 3.72
4.49
3.56
3.95
3.76		 2.64
3.11
2.60
2.79
2.82		 2.91
3.07
2.89
3.20
2.96		 1.83
2.15
2.04
1.98
1.98

The SEMs for the remaining ASVAB subtests are given in the table below. Note that the SEM computations for AI and SI are based on the observed standard deviation of the AS score, since separate scores are not reported for AI and SI.

Standard Errors of Measurement for the Non-AFQT Subtests
GS EI AI SI AS MC AO
Group P&P CAT P&P CAT P&P CAT P&P CAT P&P CAT P&P CAT P&P CAT
All 3.86 3.04 4.81 3.37 n/a 3.48 n/a 3.83 4.31 n/a 4.07 3.37 3.38 3.43
Male
Female		 3.85
3.58		 2.97
2.97		 4.64
4.35		 3.22
3.04		 n/a
n/a		 3.24
2.84		 n/a
n/a		 3.65
2.90		 4.00
3.46		 n/a
n/a		 3.98
3.59		 3.27
2.89		 3.43
3.21		 3.45
3.26
Hispanic
Non-Hispanic		 3.75
3.86		 3.19
2.92		 4.63
4.82		 3.55
3.25		 n/a
n/a		 3.28
3.42		 n/a
n/a		 3.60
3.77		 4.02
4.30		 n/a
n/a		 3.79
4.10		 3.25
3.32		 3.21
3.41		 3.26
3.45
American-Indian
Asian
Black
Pacific Islander
White		 3.67
4.63
3.52
4.05
3.61		 2.77
3.66
2.97
3.11
2.92		 4.64
5.54
4.48
4.71
4.46		 3.08
3.96
3.36
3.51
3.22		 n/a
n/a
n/a
n/a
n/a		 3.17
3.41
3.06
3.39
3.32		 n/a
n/a
n/a
n/a
n/a		 3.49
3.69
3.24
3.69
3.68		 3.91
3.89
3.68
3.97
3.81		 n/a
n/a
n/a
n/a
n/a		 3.75
4.31
3.61
3.95
3.77		 3.07
3.49
3.06
3.19
3.27		 3.20
3.48
3.19
3.20
3.29		 3.32
3.54
3.29
3.32
3.37